가우스 정수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 기본 정의
3. 가우스 소수
- 3.1. 정수에서의 가우스 소수
- 3.2. 가우스 소수의 유형
4. 유클리드 나눗셈
5. 주 아이디얼
6. 유일 인수 분해
7. 가우스 유리수
8. 최대공약수
9. 합동 및 잉여류
- 9.1. 잉여류 체
10. 원시 잉여류군과 오일러 피 함수
11. 역사적 배경
12. 응용
- 12.1. 피타고라스 수
- 12.2. 4차 잉여의 상호 법칙
13. 미해결 문제
참조

1. 개요

가우스 정수는 실수부와 허수부가 모두 정수인 복소수이다. 덧셈과 곱셈에 대해 닫혀 있으며, 복소수 체의 부분환이자 정역을 이룬다. 가우스 정수는 복소평면에서 2차원 정수 격자를 구성하며, 노름은 두 제곱수의 합으로 표현된다. 가우스 정수환의 단원은 1, -1, i, -i이며, 가우스 소수는 가우스 정수의 곱으로 나타낼 수 없는 가우스 정수를 의미한다. 가우스 정수는 유클리드 나눗셈이 가능하며, 유일 인수 분해 정역이다. 가우스 정수환은 주 아이디얼 정역이며, 최대공약수와 합동, 잉여류 등의 개념을 정의할 수 있다. 가우스 정수는 피타고라스 수 공식 유도와 페르마의 마지막 정리 연구, 4차 잉여 상호 법칙 연구 등에 응용되었으며, 가우스 소수의 분포와 관련된 미해결 문제들이 존재한다.

더 읽어볼만한 페이지

복소수 - 허수 단위
허수 단위 i는 i² = −1을 만족하는 수로, 실수 체계에서는 정의되지 않는 음수의 제곱근을 나타내며 복소수 체계의 기본 구성 요소로서 복소평면에서 90° 회전하는 효과를 가지며 1, i, -1, -i를 주기적으로 순환하는 특징을 가진다.
복소수 - 아이젠슈타인 정수
아이젠슈타인 정수는 1의 원시 세제곱근 ω를 사용하여 a + bω 꼴로 나타낼 수 있는 대수적 정수이며, 유클리드 정역을 이루어 유일 소인수분해를 갖는다.
격자점 - 역격자
역격자는 브라베 격자의 쌍대 개념으로, 해당 격자의 모든 벡터와의 내적이 정수가 되는 벡터들의 집합으로 정의되며, 결정 구조 분석 및 블로흐 정리와 관련된 브릴루앙 영역 연구에 활용되는 또 다른 브라베 격자이다.
격자점 - 아이젠슈타인 정수
아이젠슈타인 정수는 1의 원시 세제곱근 ω를 사용하여 a + bω 꼴로 나타낼 수 있는 대수적 정수이며, 유클리드 정역을 이루어 유일 소인수분해를 갖는다.

가우스 정수
개요
가우스 정수의 복소 평면상 표현
정의	실수부와 허수부가 모두 정수인 복소수
대수적 표현	a + bi (단, a, b는 정수이고, i는 허수 단위)
기호	Z[i]
관련 분야	정수론, 대수학
수학적 성질
가환환 여부	예
정역 여부	예
유클리드 정역 여부	예
주 아이디얼 정역 여부	예
유일 인수 분해 정역 여부	예
대수적 폐포	C
분수체	Q[i]
대수적 성질 (추가 정보)
노름	N(a + bi) = a^2 + b^2
단원군	{1, -1, i, -i}
관련 개념
아이젠슈타인 정수	1의 세제곱근의 정수 계수 선형 결합으로 표현되는 복소수

2. 기본 정의

가우스 정수는 다음과 같은 집합이다.^[1]

: $\mathbf{Z}[i]=\{a+bi \mid a,b\in \mathbf{Z} \}, \qquad \text{ where } i^2 = -1.$

다시 말해, 가우스 정수는 실수부와 허수부가 모두 정수인 복소수이다. 가우스 정수는 덧셈과 곱셈에 대해 닫혀 있으므로, 가환환을 이룬다. 이는 복소수 체의 부분환이며, 따라서 정역이다.

복소평면에서 가우스 정수는 2차원 정수격자를 구성한다.

가우스 정수 ''a'' + ''bi'' 의 켤레는 가우스 정수 ''a'' – ''bi'' 이다.

가우스 정수의 노름은 그 수와 그의 켤레의 곱이다.

: $N(a+bi) = (a+bi)(a-bi) = a^2+b^2.$

따라서 가우스 정수의 노름은 복소수로서의 절댓값의 제곱이다. 가우스 정수의 노름은 음이 아닌 정수이며, 두 제곱수의 합이다. 따라서 노름은 4''k'' + 3 (''k''는 정수)의 꼴을 가질 수 없다.

노름은 곱셈적이다. 즉,^[2]

: $N(zw) = N(z)N(w),$

가 모든 가우스 정수쌍 ''z'', ''w'' 에 대해 성립한다. 이는 직접적으로 보이거나 복소수의 절댓값의 곱셈적 성질을 이용하여 보일 수 있다.

가우스 정수환의 단원 (즉, 곱셈 역원이 가우스 정수인 가우스 정수)은 노름이 1인 가우스 정수, 즉 1, –1, ''i'', –''i'' 이다.^[3]

3. 가우스 소수

가우스 정수의 환은 유클리드 정역이므로, 소인수 분해가 유일하게 존재한다. '''가우스 소수'''는 다른 가우스 정수의 곱으로 표현할 수 없는 가우스 정수를 말한다. 예를 들어, (3+i)는 (2-i)(1+i)로 나타낼 수 있으므로 가우스 소수가 아니다. 하지만 (1+i)는 다른 두 가우스 정수의 곱으로 표현할 수 없다.

가우스 소수의 예는 다음과 같다: (1+i), (1+2i), (2+i), (1+4i), (2+3i), (3+2i), (4+i), (1+6i), (2+5i), (4+5i), (5+6i).

3. 1. 정수에서의 가우스 소수

일반 소수 중 4k+3 꼴의 소수는 가우스 소수이다. 예를 들어 3, 7, 11, 19 등이 있다.^[11] 4k+1 꼴의 소수는 페르마 두 제곱수 정리에 의하여 두 제곱수의 합으로 표현될 수 있으므로 가우스 소수가 아니다. 예를 들어, 5 = (2+i)(2-i) 와 같이 나타낼 수 있다.

자연수의 경우 일반 소수 중에서 a²+b² (a, b는 자연수)로 표현 가능한 소수는 가우스 소수에서 제외된다.

(a+bi)(a-bi)=a²+b²

4k+1의 꼴의 소수들은 페르마 두 제곱수 정리에 의하여 두 제곱수의 합으로 표현되어 가우스 소수에서 제외되기 때문에 자연수 소수이면서 동시에 가우스 소수인 소수들은 4k+3꼴의 형태를 갖는다.

예를 들면, '13'은 소수이지만, 13=(2+3i)(2-3i) 로 표기 가능하기 때문에 가우스 소수가 되지 않는다. 하지만 '7'은 어떠한 두 개 이상의 가우스 정수의 곱으로도 나타낼 수 없다.

가우스 정수는 단항 이데알 정역을 이루므로 유일 인수 분해 정역을 이룬다. 이는 가우스 정수가 기약원소(즉, 두 개의 단원이 아닌 원소의 곱이 아님)인 것은 소원소(즉, 소 아이디얼을 생성함)인 것과 동치임을 의미한다.

가우스 정수의 소원소는 '''가우스 소수'''로도 알려져 있다. 가우스 소수의 짝원소도 가우스 소수이다. 가우스 소수의 켤레복소수도 가우스 소수이다 (이는 가우스 소수가 실수축과 허수축에 대해 대칭임을 의미한다).

양의 정수가 가우스 소수인 것은 4로 나누었을 때 나머지가 3인 소수(즉, 4n + 3 꼴)인 것과 동치이다. 다른 소수들은 가우스 소수가 아니지만, 각각 두 개의 켤레 가우스 소수의 곱으로 나타낼 수 있다.

가우스 정수 a + bi가 가우스 소수인 것은 다음 중 하나와 동치이다.

a, b 중 하나가 0이고 다른 하나의 절댓값이 4n + 3 꼴의 소수(여기서 n은 음이 아닌 정수)인 경우
둘 다 0이 아니고 a² + b²이 소수인 경우 (이 경우는 4n + 3 꼴이 아님)

다시 말해, 가우스 정수 m이 가우스 소수인 것은 그 노름이 소수이거나, m이 단원(±1, ±i)과 4n + 3 꼴의 소수의 곱인 것과 동치이다.

따라서 소수 자연수 p의 가우스 정수에서의 인수분해에는 세 가지 경우가 있다.

p가 4로 나누었을 때 나머지가 3이면, 그것은 가우스 소수이다. 대수적 정수론의 용어로, p는 가우스 정수에서 관성 소수라고 한다.
p가 4로 나누었을 때 나머지가 1이면, 그것은 가우스 소수와 그 켤레복소수의 곱으로 나타낼 수 있으며, 둘 다 비결합 가우스 소수이다 (어느 것도 다른 것에 단원을 곱한 것이 아님). p는 가우스 정수에서 분해 소수라고 한다. 예를 들어, 5 = (2 + i)(2 − i) 와 13 = (3 + 2i)(3 − 2i) 이다.
p = 2이면, 2 = (1 + i)(1 − i) = i(1 − i)² 이다. 즉, 2는 가우스 소수의 제곱과 단원의 곱이다. 이것은 가우스 정수에서 유일한 분기 소수이다.

3. 2. 가우스 소수의 유형

가우스 소수에는 다음과 같은 세 가지 유형이 있다.

노름이 2인 것: ±(1 + i), ±(1 − i)의 4개.^[11]
노름이 4n + 1 꼴의 유리 소수인 것:
이는 4n + 1 형태의 유리 소수의 분해를 보여준다.
100 이하의 4n + 1 형태 유리 소수의 분해 (짝수인 표현은 생략):

유리 소수	분해
5	(1 + 2i)(1 − 2i)
13	(2 + 3i)(2 − 3i)
17	(1 + 4i)(1 − 4i)
29	(2 + 5i)(2 − 5i)
37	(1 + 6i)(1 − 6i)
41	(4 + 5i)(4 − 5i)
53	(2 + 7i)(2 − 7i)
61	(5 + 6i)(5 − 6i)
73	(3 + 8i)(3 − 8i)
89	(5 + 8i)(5 − 8i)
97	(4 + 9i)(4 − 9i)

4n + 3 꼴의 유리 소수와 짝인 것:
3, 7, 11, 19, 23, 31, 43, 47, 59, 67, 71, 79, … (A002145)

이는 "두 제곱수의 합으로 나타낼 수 있는 소수는 2와 4n + 1 꼴의 것에 한정된다"는 정리(페르마의 두 제곱수 정리)와 가우스 소수가 소원소인 것에 기반한다. 유리 소수의 단원 이외의 분해는 2 또는 4n + 1 형태에 한정되며, 그 분해는

:p = (m + ni)(m − ni)

꼴에 한정된다.^[11]

유리 소수가 가우스 소수인지에 대해, 2와 4n + 1 형태의 유리 소수는 두 켤레 복소수인 가우스 소수로 인수분해되므로, 실질적으로 하나의 가우스 소수의 제곱이라고 해석할 수 있다. 이 상황을 "2는 '''분기'''한다"고 표현한다. 또, 4n + 3 형태의 유리 소수는 가우스 소수이기도 하다. 이 상황을 "3은 '''관성'''한다"고 표현한다.^[11]

4. 유클리드 나눗셈

가우스 정수는 정수와 다항식처럼 유클리드 나눗셈(나머지가 있는 나눗셈)을 할 수 있다. 즉, 가우스 정수를 다른 가우스 정수로 나누었을 때 몫과 나머지를 구할 수 있다는 뜻이다. 이는 가우스 정수가 유클리드 정역임을 의미한다.

유클리드 나눗셈 알고리즘은 가우스 정수의 환에서 피제수 a와 제수 b ≠ 0를 받아 몫 q와 나머지 r을 생성하여 다음을 만족한다.

:

a=bq+r

그리고

N(r)

사실, 나머지를 더 작게 만들 수 있다.

:

a=bq+r

그리고

N(r)\le \frac{N(b)}{2}.

몫과 나머지는 반드시 유일하지 않지만, 유일성을 보장하도록 선택을 개선할 수 있다.

이를 증명하기 위해 복소수 몫 x + iy = a/b 를 고려할 수 있다. –1/2 < x – m ≤ 1/2 및 –1/2 < y – n ≤ 1/2 를 만족하는 유일한 정수 m 및 n가 존재하므로 N(x – m + i(y – n)) ≤ 1/2 이다. q = m + in 이라고 하면,

: a = bq + r,

이고

: r = b(x-m+ i(y-n)),

이며

:

N(r)\le \frac{N(b)}{2}.

열린 구간에서 x – m 과 y – n 의 선택은 유일성에 필요하다.

유클리드 나눗셈의 이 정의는 복소 평면에서 기하학적으로 해석될 수 있다(그림 참조). 복소수 ξ에서 가장 가까운 가우스 정수까지의 거리는 최대

\frac{\sqrt{2}}{2}

이다.^[4]

가우스 정수환에서의 소인수분해의 일의성은 가우스가 처음으로 증명하였다. 가우스 정수환은 노름에 관하여 유클리드 정역이기에, 다음이 성립한다.

임의의 가우스 정수 α, β (≠ 0)에 대하여

: α = βγ + δ (N(δ) < N(β))

를 만족하는 가우스 정수 γ, δ가 존재한다.

(증명) 가우스 평면에서 α/β에 가장 가까운 가우스 정수 γ를 취하면

: |α/β - γ| ≤ 1/√2 < 1

(중간 항은 한 변의 길이가 1인 정사각형의 대각선 길이의 절반)이므로, N(α - βγ) < N(β)가 되므로, δ = α - βγ로 하면 된다.

5. 주 아이디얼

가우스 정수환은 주 아이디얼 정역이며, 이는 가우스 정수환의 모든 아이디얼이 주 아이디얼임을 의미한다. 아이디얼 I는 환 R의 부분집합으로, I의 원소들의 합과 I의 원소와 R의 원소의 곱이 모두 I에 속한다. 주 아이디얼은 단일 원소 g의 모든 배수로 구성되는 경우, 즉 다음과 같은 형태를 갖는다.

: $\{gx\mid x\in G\}.$

이 경우, 아이디얼이 g에 의해 ''생성''되거나, g가 아이디얼의 ''생성원''이라고 한다.

가우스 정수 환의 모든 아이디얼 I는 주 아이디얼이다. I에서 최소 노름을 갖는 영이 아닌 원소 g를 선택하면, I의 모든 원소 x에 대해, x를 g로 유클리드 나누기한 나머지는 I에도 속하며, g의 노름보다 작은 노름을 갖는다. g의 선택으로 인해, 이 노름은 0이며, 따라서 나머지도 0이다. 즉, x = qg가 성립하는데, 여기서 q는 몫이다.

어떤 g에 대해, g에 의해 생성된 아이디얼은 g의 모든 ''연결원''(associate), 즉 g, gi, –g, –gi에 의해서도 생성된다. 다른 어떤 원소도 같은 아이디얼을 생성하지 않는다. 아이디얼의 모든 생성원은 같은 노름을 가지므로, ''아이디얼의 노름''은 생성원 중 하나의 노름이다.

6. 유일 인수 분해

가우스 정수는 단원과 가우스 소수의 곱으로 유일하게 인수분해될 수 있다. 이는 가우스 정수환이 유일 인수 분해 정역임을 의미한다. 모든 일의적 인수분해 정역과 마찬가지로, 모든 가우스 정수는 단원과 가우스 소수의 곱으로 인수분해될 수 있으며, 이 인수분해는 다음을 제외하고 유일하다.

인수의 순서
어떤 소수를 그 짝수(associated primes) 중 하나로 바꾸는 것 (단원 인수의 해당하는 변화와 함께)

만약 연관된 소수들의 각 동치류에 대해 하나의 가우스 소수를 미리 정해 놓고, 인수분해에서 이 선택된 소수들만을 사용한다면, 인수의 순서를 제외하고는 유일한 소인수분해를 얻게 된다. 위에서 설명한 선택을 사용하면, 유일한 인수분해는 다음과 같은 형태를 갖는다.

:

u(1+i)^{e_0}{p_1}^{e_1}\cdots {p_k}^{e_k},

여기서

$u$ 는 단원이다. (즉, $u \in \{1, -1, i, -i\}$ 이다.)
$e_0$ 과 $k$ 는 음이 아닌 정수이다.
$e_1, \dots, e_k$ 는 양의 정수이다.
$p_1, \dots, p_k$ 는 선택된 짝수에 따라 다음과 같은 서로 다른 가우스 소수이다.
$p_k = a_k + ib_k$ 이고 $a$ 는 홀수이고 양수이며, $b$ 는 짝수이거나,
$p_k$ 를 $2 + 2i$ 로 나눈 나머지가 1이다. (가우스의 원래 선택)^[5]

가우스 정수환은 유클리드 정역이며, 단항 이데알 정역이고, 소원분해정역(일의분해환)이다.

임의의 가우스 정수는 곱셈의 순서와 연관에 따른 차이를 제외하고 가우스 소수의 곱으로 유일하게 나타낼 수 있다는 정리가 있다.

예:

:

5 = (1 + 2i)(1 - 2i) = (2 + i)(2 - i)

는 두 가지의 소인수분해를 나타내지만,

1 + 2i

와

2 - i

,

1 - 2i

와

2 + i

가 각각 연관되어 있으므로, 이들은 같은 소인수분해로 본다.

7. 가우스 유리수

가우스 유리수의 체는 가우스 정수의 분수체이다. 이는 실수부와 허수부가 모두 유리수인 복소수이다.

가우스 정수환은 가우스 유리수에서 정수의 정수환의 정수적 폐포이다.

이는 가우스 정수가 이차 정수임을 의미하며, 가우스 유리수가 가우스 정수인 것은 다음 방정식의 해일 때이고 그 때만 성립한다.

:² +cx+d=0,

여기서 c와 d는 정수이다. a + bi는 다음 방정식의 해이다.

:²-2ax+a²+b²=0,

이 방정식이 정수 계수를 갖는 것은 a와 b가 모두 정수일 때이고 그 때만 성립한다.

8. 최대공약수

일의 인수분해 정역에서 두 가우스 정수 $a$, $b$의 최대공약수는 $a$와 $b$의 공약수 중 노름이 가장 큰 가우스 정수 $d$이다. 즉, 다음 조건을 만족한다.

$d|a$ 이고 $d|b$ 이며,
$c|a$ 이고 $c|b$ 이면 $c|d$ 이다.

여기서 "|"는 약수 관계를 나타낸다.

두 가우스 정수의 최대공약수는 유일하지 않지만, 단위를 곱한 것까지는 유일하게 정의된다. 즉, $a$와 $b$의 최대공약수 $d$가 주어지면, $a$와 $b$의 최대공약수는 $d$, $-d$, $id$, $-id$이다.

두 가우스 정수 $a$와 $b$의 최대공약수를 계산하는 방법은 여러 가지가 있다.

소인수분해: $a$와 $b$의 소인수분해를 알고 있다면, 최대공약수를 쉽게 구할 수 있다. 하지만 소인수분해는 계산하기 어려운 경우가 많다.
유클리드 호제법: 유클리드 호제법은 소인수분해보다 훨씬 쉽고 빠른 계산 방법이다. 이 방법은 각 단계에서 두 번째 가우스 정수의 노름이 감소하기 때문에 항상 종료된다.
노름의 공약수 확인: $a$와 $b$의 최대공약수의 노름은 $N(a)$, $N(b)$, 그리고 $N(a+b)$의 공약수라는 점을 이용하는 방법이다.

여러 가우스 정수의 공통된 약수를 공약수라고 한다. 공약수가 단위뿐일 때, 그 가우스 정수들은 서로소라고 한다.

최대공약수는 다음의 특징들을 가진다.

1. 복소수 사이에는 대소 관계가 정의되어 있지 않으므로, "최대"의 의미를 노름이 최대라고 해석한다.

2. 최대공약수는 유일하게 존재하지 않으나, 동치류의 차이에 따라 4개 존재하게 된다.

3. 소인수분해의 유일성이 성립하므로, "임의의 공약수는 최대공약수의 약수이다"라는 최대공약수에 기대되는 성질이 성립한다.

9. 합동 및 잉여류

두 가우스 정수 , 는 그 차가 어떤 가우스 정수 의 배수일 때, 를 법(modulus)으로 하여 합동이라고 한다. 즉, 를 만족하는 가우스 정수 가 존재하면, 로 표기한다.

를 법으로 하는 합동 관계는 동치 관계이며, 이 동치 관계에 의해 정의되는 동치류를 잉여류(residue classes)라고 한다. 잉여류의 집합은 , , 또는 등으로 표기한다.

가우스 정수 의 잉여류는 와 합동인 모든 가우스 정수들의 집합이며, 다음과 같이 나타낸다.

: $\bar a := \left\{ z \in \mathbf{Z}[i] \mid z \equiv a \pmod{z_0} \right\}$

덧셈과 곱셈은 합동과 호환된다. 즉, 이고 이면, 이고 이다. 이는 잉여류에 대해 다음과 같은 연산을 정의할 수 있게 한다.

: $\bar a + \bar b := \overline{a+b}\quad \text{and}\quad \bar a \cdot\bar b := \overline{ab}.$

이 연산들을 통해 잉여류들은 가환환을 이룬다.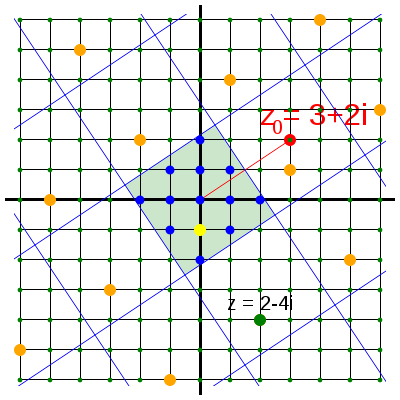

모든 가우스 정수는 어떤 모듈러스 에 대해 유일한 잉여류에 속한다. 복소평면에서 정사각형 격자를 생각하면, 모든 가우스 정수는 한 정사각형 안에 있는 유일한 가우스 정수와 합동이다. 안의 가우스 정수를 최소 잉여라고 부른다.

가우스 정수 를 법으로 하는 잉여류의 개수는 그 노름 과 같다.

예를 들어,

모듈러 에 대해서는 , 의 두 잉여류가 존재하며, 이는 체를 이룬다.
모듈러 2에 대해서는 의 네 잉여류가 존재하며, 이는 가환환을 이루지만 체는 아니다.

9. 1. 잉여류 체

가우스 정수 를 법으로 하는 잉여류 환은 가 가우스 소수일 경우 체가 된다.

만약 가 분해 소수이거나 분기 소수 인 경우 (즉, 노름 이 2이거나 4를 법으로 1과 합동인 소수인 경우), 잉여류 체는 개의 원소를 갖는다. 이는 를 법으로 하는 정수의 체와 동형이다.

반면, 가 불활성 소수 (즉, 이 4를 법으로 3과 합동인 소수의 제곱) 라면, 잉여류 체는 개의 원소를 가지며, 개의 원소를 갖는 소체의 차수 2인 확장체이다.

10. 원시 잉여류군과 오일러 피 함수

가우스 정수의 모듈에 대한 많은 정리(와 그 증명)는 모듈러스의 절댓값을 노름으로 대체하면 가우스 정수의 모듈러스로 직접 이전될 수 있다. 이는 특히 원시잉여류군(n을 법으로 하는 정수의 곱셈군)과 오일러의 피 함수에 대해 성립한다. 모듈러스 z|z^영어의 원시잉여류군은 z|z^영어와 서로소인 모든 잉여류 를 포함하는 그 잉여류의 부분집합으로 정의된다. 즉, (a|a^영어, z|z^영어) = 1이다. 명백하게, 이 시스템은 곱셈군을 구성한다. 그 원소의 개수는 ϕ(z)|ϕ(z)^영어로 표기한다(정수 n|n^영어에 대한 오일러의 피 함수 φ(n)|φ(n)^영어와 유사하게).

가우스 소수에 대해서는 ϕ(p) = |p|² − 1|ϕ(p) = |p|² − 1^영어이 즉시 따르며, 임의의 합성 가우스 정수

: $z = i^k\prod_m {p_m}^{\nu_m}$

에 대해 오일러의 곱 공식은 다음과 같이 유도될 수 있다.

: $\phi(z) =\prod_{m\, (\nu_m > 0)} \bigl|{p_m}^{\nu_m}\bigr|^2 \left( 1 - \frac 1{|p_m|{}^2} \right) = |z|^2\prod_{p_m|z}\left( 1 - \frac 1$

11. 역사적 배경

카를 프리드리히 가우스는 1832년 이차 상호 법칙에 관한 두 번째 논문에서 가우스 정수의 환을 소개했다.^[6] 이차 상호 법칙(그는 1796년에 처음으로 증명하는 데 성공했다)은 ''x''² ≡ ''q'' (mod ''p'')의 해가 존재하는지와 ''x''² ≡ ''p'' (mod ''q'')의 해가 존재하는지를 관련짓는다. 마찬가지로, 삼차 상호 법칙은 ''x''³ ≡ ''q'' (mod ''p'')의 해가 존재하는지와 ''x''³ ≡ ''p'' (mod ''q'')의 해가 존재하는지를 관련짓고, 사차 상호 법칙은 ''x''⁴ ≡ ''q'' (mod ''p'')와 ''x''⁴ ≡ ''p'' (mod ''q'') 사이의 관계를 나타낸다. 가우스는 사차 상호 법칙과 그 보조 정리가 보통의 정수에 대한 명제로 표현하고 증명하는 것보다 "복소 정수"(즉, 가우스 정수)에 대한 명제로 표현하고 증명하는 것이 더 쉽다는 것을 발견했다.

그는 각주에서 아이젠슈타인 정수가 삼차 상호 법칙에 대한 결과를 진술하고 증명하는 자연스러운 영역이며, 정수의 유사한 확장이 고차 상호 법칙을 연구하는 데 적합한 영역임을 나타낸다.

이 논문은 가우스 정수를 소개하고 그것이 유일 인수 분해 정역임을 증명했을 뿐만 아니라, 현재 대수적 정수론에서 표준적인 용어인 노름, 단위, 일차, 동류 등의 용어를 도입했다.

12. 응용

가우스 정수는 수학의 여러 분야에서 응용된다.

가우스 정수를 이용하면 서로소인 피타고라스 수를 표현하는 공식을 유도할 수 있다. (자세한 내용은 피타고라스 수 하위 섹션 참조)

또한, 가우스는 가우스 정수환을 연구하여 4차 잉여의 상호 법칙을 공식화하였다. 이 법칙은 정수 n과 소수 p에 대해 x⁴ ≡ n (mod p)가 해를 갖는 경우를 설명한다. 가우스는 이 법칙의 증명을 공표하지 않았지만, 그의 제자인 아이젠슈타인이 증명을 발표했다.^[13] (자세한 내용은 4차 잉여의 상호 법칙 하위 섹션 참조)

12. 1. 피타고라스 수

가우스 정수를 이용하여 서로소인 피타고라스 수를 표현하는 공식을 유도할 수 있다. 서로소인 피타고라스 수는 모두 다음 공식으로 나타낼 수 있다.

:(''m''² - ''n''², 2''mn'', ''m''² + ''n''²)

(''a'', ''b'', ''c'')를 원시 피타고라스 수라고 하자. 즉,

:(''a''² + ''b''² = ''c''²)

이고 ''a'', ''b'', ''c''는 서로소이다. ''a''와 ''b''는 홀짝이 다르고, ''c''는 홀수이다. 좌변을 인수분해하면

:(''a'' + ''bi'')(''a'' - ''bi'') = ''c''²

을 얻는다. 가우스 소수 ''a'' + ''bi''와 ''a'' - ''bi''는 서로소이다. 실제로, 어떤 가우스 소수 α가 둘 모두를 나눈다고 하면, 그 합과 차도 나누므로, 2''a''와 2''b''를 나눈다. ''a''와 ''b''는 서로소이므로, α는 2를 나눈다. α는 ''c''도 나누므로, ''c''가 홀수라는 것과 모순된다. 따라서 그러한 가우스 소수 α는 존재하지 않는다.

서로소인 ''a'' + ''bi''와 ''a'' - ''bi''의 곱이 제곱수이므로, 각각 제곱수와 동류이다(여기서 소인수분해의 유일성을 사용했다). 예를 들어 ''a'' + ''bi'' = (''m'' + ''ni'')²라고 하면, 위의 공식을 얻는다. 동류의 차이는 부호의 차이 또는 ''a''와 ''b''의 교환만을 준다. 실제로 공식이 원시 피타고라스 수를 주려면, ''m'', ''n''은 서로소이고 홀짝이 다르며, ''m'' > ''n''이어야 한다.

12. 2. 4차 잉여의 상호 법칙

가우스가 가우스 정수환을 연구한 동기 중 하나는 다음과 같은 문제였다.

정수 n과 소수 p에 대해 합동식 x⁴ ≡ n (mod p)가 해를 갖는 것은 어떤 경우인가?

이 문제는 유리 정수환의 세계에서만 생각하는 것이 아니라, 가우스 정수환에서 생각하는 것이 본질적이다. 오늘날 4차 잉여의 상호 법칙이라고 불리는 공식이 하나의 해답을 제시하고 있다. 가우스는 1828년과 1832년 두 차례에 걸쳐 4차 잉여에 관한 자신의 연구를 정리한 논문을 발표했다. 후자의 논문에서 가우스 정수환에서의 기약 분해의 유일성을 증명하고, 4차 잉여의 상호 법칙을 공식화했다. 가우스 자신은 상호 법칙의 증명을 공표하지 않았지만, 가우스의 제자인 아이젠슈타인이 1844년에 증명을 공표했다.^[13] 아이젠슈타인은 더 나아가 3차 잉여의 상호 법칙의 공식화와 증명을 수행했다. 4차 잉여를 생각할 때 ℤ에 1의 원시 4제곱근(허수 단위)을 추가한 환을 생각할 필요가 있었던 것처럼, 3차 잉여를 생각하기 위해서는 ℤ에 1의 원시 3제곱근을 추가한 환(오늘날 아이젠슈타인 정수환이라고 불린다)을 생각할 필요가 있다. 참고로, 나중에 공표된 가우스의 유고에 따르면, 가우스는 이미 4차 잉여의 상호 법칙의 증명을 제시하고,^[14] 3차 잉여에 대해서도 선구적인 연구를 했던 것을 알 수 있다.

13. 미해결 문제

대부분의 미해결 문제는 평면에서 가우스 소수의 분포와 관련이 있다.

가우스 원 문제는 가우스 정수 자체를 다루지는 않지만, 원점을 중심으로 하는 주어진 반지름의 원 안에 있는 격자점의 수를 묻는다. 이는 주어진 값보다 작은 노름을 가진 가우스 정수의 수를 결정하는 것과 같다.

가우스 소수에 대한 추측과 미해결 문제들도 있다. 그중 두 가지는 다음과 같다.

실수축과 허수축에는 3, 7, 11, 19, ... 와 그 켤레인 무한한 가우스 소수 집합이 있다. 무한히 많은 가우스 소수를 포함하는 다른 직선이 있는가? 특히, 1 + ''ki'' 형태의 가우스 소수가 무한히 많은가?^[7]
가우스 소수를 발판으로 삼고 일정하게 경계가 지정된 길이의 발걸음을 사용하여 무한대로 걸어갈 수 있는가? 이것은 가우스 해자 문제로 알려져 있으며, 1962년 Basil Gordon에 의해 제기되었고 여전히 미해결 상태로 남아 있다.^[8]^[9]

참조

_[1] harvtxt
_[2] harvtxt
_[3] harvtxt
_[4] harvtxt
_[5] harvtxt
_[6] harvtxt
_[7] 서적 Ribenboim, Ch.III.4.D Ch. 6.II, Ch. 6.IV (Hardy & Littlewood's conjecture E and F)
_[8] 논문 A stroll through the Gaussian primes
_[9] 서적 Unsolved problems in number theory Springer-Verlag
_[10] 서적 19世紀の数学整数論共立出版
_[11] 서적 Unsolved Problems in Number Theory Springer-Verlag
_[12] 서적 フェルマーの大定理整数論の源流筑摩書房
_[13] 서적 数論を学ぶ人のための相互法則入門牧野書店
_[14] 서적 数学をつくった人びと早川書房

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com